One dimensional heat equation: implicit methods
Contents
11. One dimensional heat equation: implicit methods#
11.1. Introduction#
For convenience, we start by importing some modules needed below:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('../styles/mainstyle.use')
In the previous notebook we have described some explicit methods to solve the one dimensional heat equation;
where \(T\) is the temperature and \(\sigma\) is an optional heat source term.
In all cases considered, we have observed that stability of the algorithm requires a restriction on the time step proportional to \(\Delta x^2\). As this is rather restrictive, we focus here on some implicit methods and see how they compare.
11.2. Backward Euler method#
We begin by considering the backward Euler time advancement scheme in combination with the second-order accurate centered finite difference formula for \(d^2T/dx^2\) and we do not include the source term for the stability analysis.
We recall that for a generic ordinary differential equation \(y'=f(y,t)\), the backward Euler method is,
In our case, the discretization is therefore,
In matrix notation this is equivalent to:
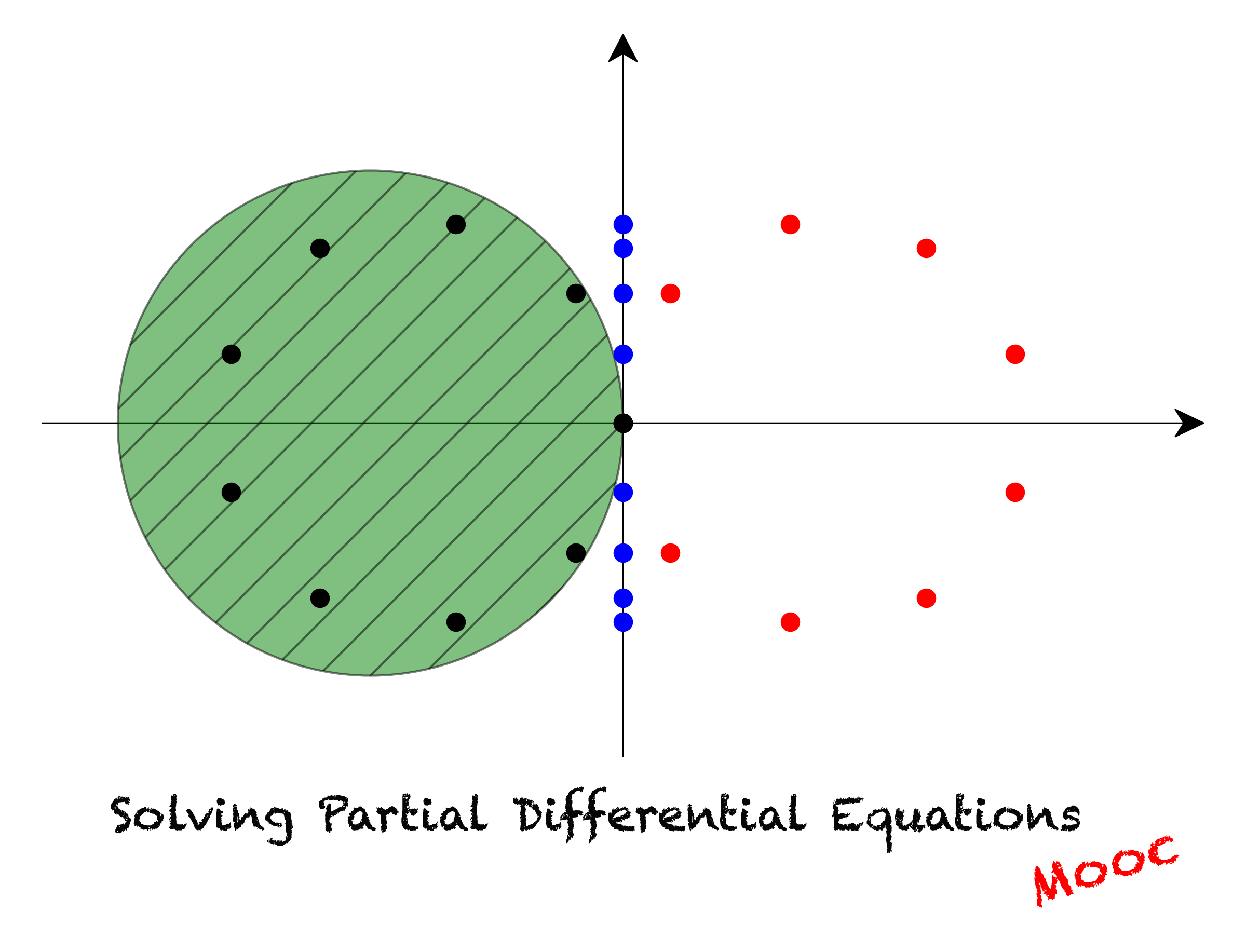
where \(I\) is the identity matrix. If we adopt Dirichlet boundary conditions, the matrix \(A\) is identical to its counterpart for the forward Euler scheme (see previous notebook). For reference, the eigenvalues \(m_k\) of \(A\) are real and negative:
If we diagonalize \(A\) and denote by \(\boldsymbol z=(z_1,\ldots,z_{nx-2})\) the coordinates of \(\boldsymbol T\) in the basis of eigenvectors, we have:
where \(\Lambda\) is the diagonal matrix containing the eigenvalues of \(A\). Each of the \(nx-2\) decoupled equations may therefore be written as:
Since \(m_k < 0\; \forall k\), all the coordinates \(z_k\) remain bounded and the algorithm is unconditionally stable.
We can also examine the stability of the algorithm for the case of periodic boundary conditions using the modified wavenumber analysis. We adopt the same notations as in the previous notebook and get the same expression for the evolution of the Fourier modes,
with the modified wavenumbers being real and defined by,
Because all the coefficients \(-\alpha k_m'^2\) are real and negative, the Fourier components remain bounded if we discretize eq. (48) using the backward time integration method. The algorithm is therefore also unconditionally stable in the case of periodic boundary conditions.
11.3. Crank-Nicolson method#
A popular method for discretizing the diffusion term in the heat equation is the Crank-Nicolson scheme. It is a second-order accurate implicit method that is defined for a generic equation \(y'=f(y,t)\) as:
You should check that this method is indeed second-order accurate in time by expanding \(f(y^{n+1}, t^{n+1})\) in Taylor series.
For the heat equation, the Crank-Nicolson method yields the following expression:
In matrix form (assuming Dirichlet boundary conditions), this is equivalent to:
with \(A_{cn}\) being the same matrix as in the previous section except for the prefactor that is now \(\displaystyle\frac{\alpha \Delta t}{2\Delta x^2}\).
Both sides of the equation can be diagonalized using the same eigenvectors. Therefore, the coordinates of \(\boldsymbol{T}\) in the basis of eigenvectors evolve according to:
Since \(m_k < 0\; \forall k\), all the coordinates \(z_k\) remain again bounded and the algorithm is unconditionally stable.
In the case of periodic boundary conditions, we may again study the stability of the method by decomposing the temperature field in Fourier modes. According to eq. (49) we get:
or equivalently
As the denominator is always larger than the numerator, all the Fourier modes remain bounded and we conclude again the algorithm is unconditionally stable.
Let’s use these implicit methods and compare them with the forward Euler method that we used in the previous notebook.
11.4. Numerical solution#
To test the above numerical methods we use the same example as in the previous notebook. The source term in eq. (47) is \(\sigma = 2\sin(\pi x)\) and the initial condition is \(T_0(x) = \sin(2\pi x)\). To make the algorithms work a bit more, we increase the diffusivity parameter to \(\alpha=0.1\). The exact solution of the equation is,
To get started we import some helper functions. The corresponding modules are part of the course’s module directory and its path has to be added to the Python search path. The only exception is the pde_module that is located in the current notebook’s directory, as it is not useful for other notebooks.
import sys
sys.path.insert(0, '../modules')
# Euler step functions
from steppers import euler_step
# Function to compute an error in L2 norm
from norms import l2_diff
# Function to compute d^2 / dx^2 with second-order
# accurate centered scheme
from matrices import d2_mat_dirichlet
# Function for the RHS of the heat equation and
# exact solution of our example problem
from pde_module import rhs_heat_centered, exact_solution
Physical and grid parameters to achieve a precision smaller than \(10^{-6}\) in L2-norm:
# Physical parameters
alpha = 0.1 # Heat transfer coefficient
lx = 1. # Size of computational domain
ti = 0.0 # Initial time
tf = 5.0 # Final time
# Grid parameters
nx = 513 # number of grid points
dx = lx / (nx-1) # grid spacing
x = np.linspace(0., lx, nx) # coordinates of grid points
To evaluate how much faster we can get our solution with the implicit scheme, we will time our algorithms. The first one we consider is the forward Euler scheme using the Euler step function. We know that in that case, we have to use a Fourier number \(F<0.5\) (see the notebook 04_03_Diffusion_Explicit).
Forward Euler method in component form:
# Time parameters
fourier = 0.49 # Fourier number
dt = fourier*dx**2/alpha # time step
nt = int((tf-ti) / dt) # number of time steps
# Solution parameters
T0 = np.sin(2*np.pi*x) # initial condition
source = 2*np.sin(np.pi*x) # heat source term
sol = exact_solution(x, tf, alpha) # Exact solution
T = np.empty((nt+1, nx)) # Allocate storage for the solution
T[0] = T0.copy() # Set the initial condition
%%timeit
for i in range(nt):
T[i+1] = euler_step(T[i], rhs_heat_centered, dt, dx, alpha, source)
2.69 s ± 53.3 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
diff_exact = l2_diff(T[-1], sol)
print(f'The L2-error made in the computed solution is {diff_exact}')
print(f'Time integration required {nt} steps')
The L2-error made in the computed solution is 2.0316335156901795e-07
Time integration required 267493 steps
Using \(nx=513\), the accuracy is below our set target but it requires \(267493\) time steps.
Forward Euler method in matrix form
For the implicit methods, we need to perform matrix multiplications to time advance the solution. As an extra test, we also evaluate the efficiency of the forward Euler scheme in matrix form to assess the time penalty required by the matrix multiplications.
In this case, the time stepping is performed with:
The needed matrices are computed as follows:
# d^2 / dx^2 matrix with Dirichlet boundary conditions
D2 = d2_mat_dirichlet(nx, dx)
# I+A matrix
M = np.eye(nx-2) + alpha*dt*D2
Timing of the solution:
T[0] = T0.copy() # Set the initial condition
%%timeit
for i in range(nt):
T[i+1, 1:-1] = np.dot(M, T[i, 1:-1]) + source[1:-1]*dt
# Set the boundary values
T[-1,0] = 0.
T[-1,-1] = 0.
4.82 s ± 273 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
diff_exact = l2_diff(T[-1], sol)
print(f'The L2-error made in the computed solution is {diff_exact}')
print(f'Time integration required {nt} steps')
The L2-error made in the computed solution is 2.0316334259879517e-07
Time integration required 267493 steps
As expected, the algorithm in matrix form gives nearly identical results as in component form. The tiny differences are due to round-off errors.
We note that the algorithm implemented in a matrix form is two times slower than that implemented in a component form.
Let’s turn our attention to the implicit algorithms. For these, there is no limit on the time step but we still want to achieve the desired precision.
Backward Euler method
For this method, we have determined empirically that the desired precision is achieved by setting the Fourier number to \(F=10\). To check this, let’s apply the algorithm:
fourier = 10 # Fourier number
dt = fourier*dx**2/alpha # time step
nt = int((tf-ti) / dt) # number of time steps
# I-A matrix
M = np.eye(nx-2) - alpha*dt*D2
Minv = np.linalg.inv(M)
T = np.empty((nt+1, nx)) # Allocate storage for the solution
T[0] = T0.copy() # Set the initial condition
Timing of the solution:
%%timeit
for i in range(nt):
T[i+1, 1:-1] = np.dot(Minv, T[i, 1:-1] + source[1:-1]*dt)
# Set boundary values
T[-1,0] = 0
T[-1,-1] = 0
232 ms ± 21.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
diff_exact = l2_diff(T[-1], sol)
print(f'The L2-error made in the computed solution is {diff_exact}')
print(f'Time integration required {nt} steps')
The L2-error made in the computed solution is 2.6677344754046066e-07
Time integration required 13107 steps
Using the backward Euler method, the number of time steps has been reduced by a factor of 20 and the execution time by a factor 10 compared to the forward Euler method in component form!
Crank-Nicolson method
The last method we consider here is the Crank-Nicolson method. This methods is second-order accurate in time so we can expect even better improvement. After some testing, we have determined that the Fourier number could be raised to a value of \(55\). Let’s check this:
fourier = 55 # Fourier number
dt = fourier*dx**2/alpha # time step
nt = int((tf-ti)/dt) # number of time steps
# I-0.5*A matrix + inverse
A = np.eye(nx-2) - 0.5*alpha*dt*D2
Ainv = np.linalg.inv(A)
# I+0.5*A matrix
B = np.eye(nx-2) + 0.5*alpha*dt*D2
# (I+0.5A)^{-1} * (I-0.5*A)
C = np.dot(Ainv, B)
T = np.empty((nt+1, nx)) # Allocate storage for the solution
T[0] = T0.copy() # Set the initial condition
%%timeit
scn = np.dot(Ainv, source[1:-1]*dt)
for i in range(nt):
T[i+1, 1:-1] = np.dot(C, T[i, 1:-1]) + scn
# Set boundary values
T[-1,0] = 0
T[-1,-1] = 0
40.2 ms ± 7.17 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
diff_exact = l2_diff(T[-1], sol)
print(f'The L2-error made in the computed solution is {diff_exact}')
print(f'Time integration required {nt} steps')
The L2-error made in the computed solution is 7.08219117721633e-08
Time integration required 2383 steps
The number of time steps has been further reduced by a factor of 5 and the execution time is approximately 30 times faster than that with the forward Euler method!
11.5. Summary#
In this notebook we have discussed implicit discretization techniques for the the one-dimensional heat equation. These are particularly useful as explicit scheme requires a time step scaling with \(dx^2\). We have shown that the backward Euler and Crank-Nicolson methods are unconditionally stable for this problem. Although they require more complex arithmetical operations than explicit schemes, they result in very significant reduction in computational cost. These reductions are problem dependent because achieving enough accuracy depends on several factors. However, the discussion indicates that it is always important to explore the various algorithms when trying to solve a numerical problem and there is vast literature available to do this.